在小学阶段，随着学习的深入，接触到的数学解决问题策略也会越来越多。掌握各种解决问题的策略，对数学学习非常重要，能够培养学生的数学思维，发展数学关键能力。现就图形与几何领域，关于小学数学解决问题的策略做一个梳理：

图形与几何领域，小学数学解决问题中的基本策略分别是：画图策略、转化策略、列表策略、枚举策略。

画图策略在解题过程中，运用画图的方法，画出与题意相关的示意图，借助示意图来帮助推理、思考，这是小学数学解决问题中最常用的一种策略。常见的画图方式有：线段图、集合图等。将疑难问题的文字“翻译成图”，能够立竿见影地理清思路，找到解题策略。

例：水果批发店里香蕉有60箱，苹果的箱数是香蕉的3倍，苹果和香蕉一共有多少箱?先把线段图补充完整，再计算。

   分析：1+3=4,4×60=240（箱）

画线段图可以帮助孩子快速理清各种量之间的逻辑关系，提高解题效率。

转化策略转化也是小学数学解决问题中常用的一种方法，能把较复杂的问题转化为简单问题，能把未知的问题变为已知的问题。

例如：

1、推导平行四边形的面积公式时，将平行四边形的面积转化为长方形的面积来计算。

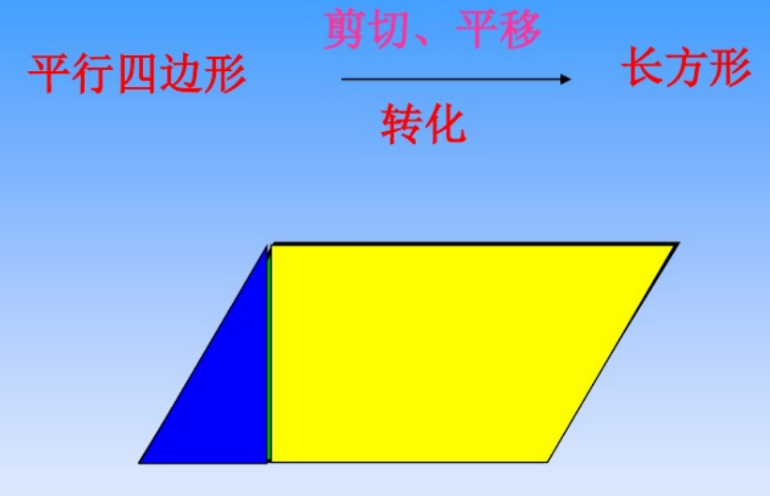
2、推导三角形的面积公式时，将三角形面积转化为等底等高的平行四边形面积的一半。

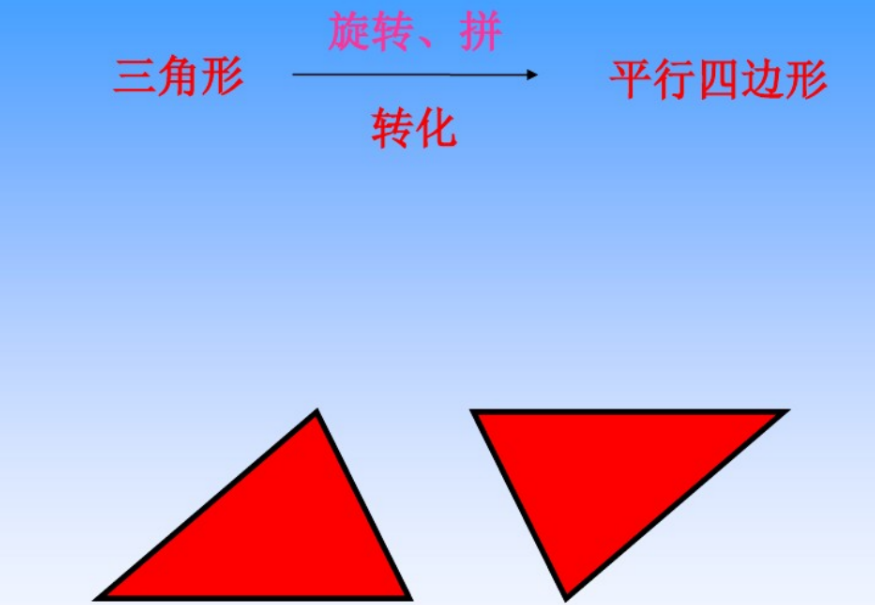
3、推导梯形面积公式时，将梯形面筋转化为平行四边形面积的一半。

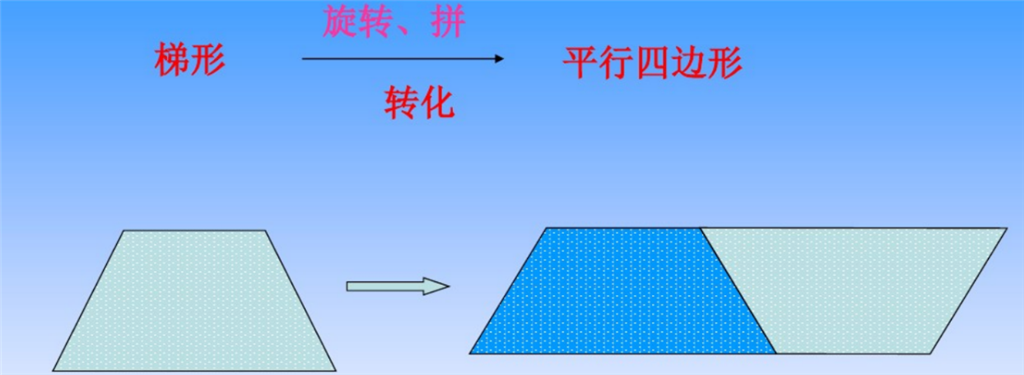
列表策略，是将问题的条件信息用表格的形式列举出来，便于从中发现问题、分析数量关系，从而排除非数学信息的干扰，同时也便于找到解决问题的方法。

例：张大伯家种了15行梨树，17行桃树和8行苹果树，梨树每行17棵，桃树每行8棵，苹果树每行9棵，梨树和桃树一共有多少棵？（列表整理条件，再解答）

17×15+8×17
=255+136
=391（棵）
答：树和桃树一共有391棵．

【分析】根据题意：梨树有15行，每行17棵，桃树有17行，每行8棵，苹果树有8行，每行9棵，由此列出表格；
根据乘法的意义，梨树的棵数是17×15棵，桃树一共有8×17棵，把它们相加即可求出树和桃树一共有多少棵．

枚举策略在解决一些特殊问题时，有时候没有办法列算式，这个时候列举出被研究对象的所有可能情况，则能使问题比较容易地获得解决。和列表策略一样，在枚举时也要做到有序思考，这样才能做到不重不漏。

例：用36个面积是1平方厘米的正方形拼成长方形，有多少种不同的拼法？它们的周长各是多少？

分析：从宽为1开始考虑：

    同一个知识内容，不同的理解角度、不同的思维方式，所选择的解题策略也会有所不同。在平时教学中，要尽可能多地让学生掌握解决问题的一些策略，在遇到具体问题时灵活判断和选择相关策略进行综合运用，从而提高解决问题的能力，提高解题效率。